Discovering Group Theory, Day 4

Realizing that there was much to be gained from using now familiar cyclic groups to introduce more group properties, we postponed the exploration of dihedral groups and instead spent the day exploring.

• The review of group properties
  • After reviewing the structure of particular examples of cyclic groups (C₁, C₂, C₃, C₄, and C₆) students extrapolated the properties of C_n, which led us to the formal definition of cyclic groups.
• Modular Addition and (Z_n,+_n)
  • We built on our existing knowledge of how to calculate the hour reading of a clock to motivate modular addition. Students were asked to come up with a general mathematical formula which can be used to do the calculations.
  • Working in pairs, students then investigated whether (Z₄,+4) forms a group by checking if it satisfies the four axioms and constructing the Cayley table.  This exercises broadened our understanding of group “multiplication,” which was originally introduced as a way to represent compounding effects of subsequent rotations of a polygon. It became clear why we have been using quotes around the word multiplication.

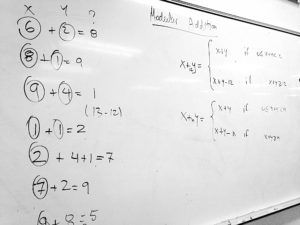
• • After comparing C₄ and Z_4, we introduced the idea of a group isomorphism.
• What is Not a Group? Students wanted to know more about when a set and a “product” do not form a group, so we went through a couple of examples in which one or more of the four axioms is violated (especially associativity).